What is a p-value?
I'll answer that question, explain a statistical test you might not have heard of, and introduce you to my new obsession: bridge.
After leaving my last job, I started playing a lot of contract bridge (or “contact bridge” as it’s called in my family, as games tend to get heated). I recently participated in a regional bridge tournament. I was inspired to write this post about p-values when I found myself in what I thought was a very unlikely situation during a bridge session.
A crash course in bridge
I could talk bridge all day, but I know it’s not for everyone. Given that, I’ll try to minimize the background for this article. Bridge is a trick-taking card game played with a standard deck of 52 cards. There are four players seated around the table: North, East, South, and West. North and South are partners, and East and West are partners. Each hand is preceded by an auction in which the players bid on 1) how many tricks they think they can win, and 2) which suit is the trump suit. For example, if North-South wins the auction with a bid of 4 hearts, then they claim that they will take 6 + 4 = 10 tricks with hearts as trump. (You add 6 because there are 52/4 = 13 total tricks, so it doesn’t make sense to proclaim that you’ll take fewer than half.)
The weird thing about bridge (well, one weird thing) is that only three of the four players play each hand. One person from the team that wins the auction plays the hand. That person is called the “declarer.”1 The declarer’s partner is called the “dummy,” and the dummy’s hand is placed face up after the opening lead by the defense. The declarer then plays both hands, concealing their own. All eyes are on you as the declarer, so that is the most exciting and stressful position to be in. For concreteness, suppose that North is the declarer. This means that South, North’s partner, is the dummy, while East and West play defense. Defense always plays the first card, and they lead into the dummy. Therefore, East would lead in this case. As soon as East plays their first card, South reveals their hand, and then play continues clockwise around the compass (with North playing both North’s and South’s hands). After all 13 tricks are played, you count how many tricks the declarer took and award points according to how they fared against their bid.
My unlikely experience
So what does this have to do with p-values? As I said above, bridge is most exciting when you are the declarer. In one of my games during the recent tournament, my team played 24 hands, and I noticed that I was starting to get bored. It turns out that I was the declarer on only two of the 24 hands! Two out of 24 is 8.3%, which seemed like a very small percentage to me. Since North, East, South, and West are just names, you expect each player should declare 25% of the time in the long run. This made me wonder if chance was to blame, or rather if something about the bidding habits of the people at the table skewed the results.
Statistics gives us a way of understanding how unlikely experiences like my bridge game are. Let’s assume that North really should play 25% of hands. In that case, the proportion of hands that North plays out of N = 24 random deals is approximately normally distributed. This is a consequence of the central limit theorem. The mean of that normal distribution is π = .25, and the standard deviation is
Knowing this, we can compute the z-score of the sample proportion p = 2/24 = 8.3%:
This means that the observed proportion of 2/24 hands is almost two standard deviations below the mean of 6/24 hands. The next step is to convert this z-score into a p-value. The p-value is the area under the standard normal (i.e., bell-shaped) curve to the left of z = -1.889. You can compute it Excel with the function NORM.S.DIST(-1.889, 1). The 1 means that you want the cumulative probability (i.e., area) and not the height of the curve at that point. Entering that function returns a p-value of about .0297 (cf., picture below).

The next question is, how do we interpret the p-value? Before getting to that, it’s best to explain the context in which p-values most often arise. Hypothesis testing is the branch of statistical inference wherein you collect samples from a population to test an assumption about the population. In this case, the null hypothesis is that the true proportion of hands with North as declarer is 25%. The alternative hypothesis—based on our observation—is that North actually declares less than 25% of the time. A good real-life example is a clinical trial for a drug. In that case, you have a treatment and control group. The null hypothesis is that there is no difference in outcomes (measured however you want) between those two groups. The alternative hypothesis is that the treatment group fares better than the control group. In either case, the p-value is interpreted as follows:
Assuming that the null hypothesis is true, there is a p% chance that a random sample of this size would be as extreme as this sample.
Applied to the bridge case: Assuming that North declares on 25% of hands, there is a 2.97% chance that North would declare two or fewer times in a game with 24 hands. The 24 hands part is critical; the standard deviation of the sampling distribution depends on N, the number of hands. The more hands you play, the more unlikely it would be for North to declare in fewer than 8.3% of hands. In a hypothesis test, you typically have some cutoff—called α—that you compare to the p-value. For example, if α = .01, then you would say that a p-value less than 1% is just too unlikely to believe. The only possible conclusion is that your assumption—the null hypothesis—must be false. Depending on the context, α can be .001, .01, .05, or sometimes .1.
There are a few common misconceptions about the p-value. The first is that it depends on α. As we saw, you can define the p-value without any reference to α, which is simply your line in the sand for what constitutes “beyond a reasonable doubt.” Another common misconception is that the p-value is the probability that the null hypothesis is true. That’s not right. All the p-value tells you is the probability of observing your sample, if the null hypothesis is true. Finally, some people claim that the smaller the p-value, the stronger the effect (in a treatment/control scenario). This is also not true. The p-value just measures how unlikely it is to observe a sample. Suppose you knew that a drug reduced someone’s cholesterol by an average of 15 mg/dL. If you repeatedly ran controlled experiments, you could make the p-value as small as you want by increasing the sizes of the treatment and control groups (thereby reducing variability). However, the magnitude of the effect will always be 15 mg/dL, on average, regardless of the p-value.
Another perspective: goodness of fit
With a p-value of under 3%, it’s tempting to argue that declaring on two out of 24 hands is too rare to attribute to chance.2 However, I didn’t share all the details of my game. Of the 24 hands, I (North) declared twice, East five times, South eight times, and West nine times. As discussed, each player expects to be declarer on approximately 25% of hands. There’s another statistical test—χ-square goodness of fit—which can be used to analyze the distribution of categorical variables. This test works by comparing the observed counts of each possible value of a variable to the expected counts (6 each for North, South, East, and West in our case). To avoid positive and negative differences offsetting, each error is squared. The squared differences are then divided by the expected count and added together. (This is not unlike linear regression, which I discussed in this previous post.) The result is a single number called the χ-square statistic. This number is always positive, and it captures how far away the distribution of a variable is from what is expected. Looking at the table below, we see that χ-square = 5.0 in this case.

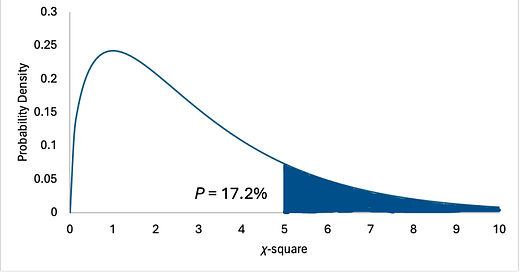
To compute a p-value, we need to know what type of distribution χ-square follows. The central limit theorem says that, for each player, the square root of Column F in the above picture converges to the standard normal normal as N increases.3 This makes χ-square the sum of squares of normally distributed variables. Shockingly, such sums follow a neat distribution called the χ-square distribution (hence the name of the statistic/test). Once you know that, then the calculation of the p-value and its interpretation are exactly the same. To calculate the p-value, you can type
=1 - CHISQ.DIST(5,3,1)in Excel. 5 is the value of the χ-square statistic. 3 is the degrees of freedom (number of players - 1) and 1 means cumulative, as with NORM.S.DIST. We have to subtract the value from 1 because now the extreme side is the right tail, not the left tail.

Which test is right?
Notice that the p-value from the χ-square test is much larger: 17.2%. This number is large enough that we would not be able to reject the null hypothesis, which is that each player plays 25% of the hands. So, on the one hand, the first test says that it is very unlikely (about 3 out of 100) that North would play zero, one, or two out of 24 hands. On the other hand, the χ-square test says that an arrangement as uneven as (N, E, S, W) = (2, 5, 8, 9) is not all that rare: it would happen more than one in six times that you play 24 hands.
This begs the question, which test is right? The short answer is that they’re both right. They’re just answering different questions. In the first case, I zoomed in on the experience of North. From North’s perspective, it’s true that it’s very rare to declare two or fewer times out of 24 hands. However, declaring is a zero-sum game (well, I guess a 24-sum game): if any of the other seats declare more times than expected, that means someone has to declare fewer times than expected. The χ-square test considers all four hands together. When you do that, the arrangement (2, 8, 9, 5) is seen to be not that pathological. In fact, I played six times during the tournament, so the chances are good that I would see some declarer distribution with p = .172 at least once. Reflecting on the tournament now, I can’t remember the number of times I declared in any of the other sessions. You could argue that I engaged in “p hacking” by focusing on the one game in which I declared only twice. p hacking is a dishonest (yet common) approach to statistical analysis in which you take multiple samples until you get a p-value that supports the conclusion you want to draw.
To close, I want to clarify one thing about the χ-square statistic. It reduces the deviation from the expected counts for all players into a single number. For example, (3, 3, 9, 9) has a higher χ-square value of 6.0 (thus, a lower p-value), even though no one declared two or fewer times. If you wanted to get the exact probability of someone declaring two or fewer times, you would apply the multinomial distribution, which models the different ways you can add up four numbers to get 24. This is tricky, though, because it’s difficult to systematically list the arrangements (N, E, S, W) that have a minimum value of 0, 1, or 2 in one of the hands.4 Instead, I simulated 500 sessions of 24 hands and noted 1) the percentage of sessions that each player played two or fewer hands, and 2) the percentage of sessions that each of 0, 1, 2, 3, 4, 5, and 6 was the minimum number of hands declared by any player. (The minimum can’t be greater than 6 because the average is 6.) As you see below, the minimum number of hands played was two or fewer in 16.8% of the 500 sessions, which is slightly less than the χ-square test. I re-ran this experiment another ~30 times, and the average was closer to 15.6%.

That’s all for today. Thank you for reading and indulging my bridge obsession. Please subscribe and share if you enjoyed this. Most importantly, please let me know if you’re looking for a bridge partner.
The declarer is the first person on the declaring team to mention the ultimate trump suit in the auction. For example, if North opens the bidding with 1 heart, they would play the hand if North-South ends up winning the auction with hearts as the trump suit. This is true even if South makes the final bid of 4 hearts.
Some possible explanations: the hands aren’t random, our bidding or our opponents bidding is unusual, etc.
Briefly, if you convert the counts to frequencies, you get a binomial distribution, and then it’s easier to see how to apply CLT. If you want more rigor, don’t read blogs. (Just kidding… here’s a proof.)
The “stars and bars” method tells you that there are 2,925 (= 27 choose 3) ways that N-E-S-W can share declarer in 24 hands. There are probably several hundred that have at least one 0, 1, or 2 in one of the positions. I was not up to the task of enumerating them.