Should you purchase mortgage points?
A net present value (NPV) framework for analyzing mortgage points like a corporate finance investment decision
Let me start by saying that I’m not going to answer the question in the title. You shouldn’t take financial advice from a math blogger. However, I will give you a framework for thinking about the question.
What are mortgage points?
I got an email offer a while back to switch to biweekly mortgage payments of 50% of my normal payment. The bank claimed it would shave 7 years (or whatever) off my mortgage. Wow — sometimes it’s easy to forget the power of compound interest. Just by making half my payment a little early, I can reduce the amount of interest I pay and pay off the loan faster. Seems like a no-brainer. Then it hit me: 52 weeks in a year equals 26 biweekly payments of 50%, which equals 13 payments of 100% (i.e., one more than you would otherwise make in a year.) To paraphrase the bank’s offer: “If you pay off your mortgage early, you can pay off your mortgage early!”
Given shenanigans like that, it’s easy to be skeptical of offers from financial institutions. However, there is at least one offer that deserves a closer look: (discount) mortgage points. Purchasing mortgage points means making a one-time cash payment when you buy your house to reduce the interest rate. In other words, it is a way to pre-pay some of your mortgage interest.
Here’s an example. Suppose that you borrow $250,000 to finance a home purchase. A 30-year mortgage at 6% interest would have a monthly payment of $1,498.88. (See my inaugural post on mortgage payments, which includes a handy workbook for calculating your own amortization table.) You may be able to reduce your monthly payment by pre-paying interest in increments of “points.” Usually, one point costs 1% of the loan amount, and it may earn you a rate reduction of 12.5 - 25 basis points (BP).1 If it’s 25 basis points, then you would have the following options:

Are mortgage points worth it?
Ask a broker (or Investopedia) about mortgage points, and they’ll talk to you about the payback period. By definition, this is the number of payments you need to make before the cumulative monthly savings exceed the cost of the points. In the example above, you save $39.95 each month if you purchase one point. At a cost of $2,500 per point, it would take you (2,500 / 39.95) = 63 months to “break even”. Therefore—they claim—you have to keep your house for a minimum of 5 years and 3 months to justify the purchase of points.
If you’re a finance person reading this, then steam is probably coming out of your ears. The problem with payback period is that it completely ignores the time value of money (TVM). Remove the house from the equation. If I offered to pay you $39.95 each month for the next 5+ years in exchange for $2,500 now, would you take that deal? Of course not. I would be robbing you of the opportunity to do anything with that $2,500 over the 5 years of the loan. To sweeten the deal, I would have to compensate you for tying up the $2,500 (not to mention inflation, the high risk of lending money to a blogger, etc.) The compensation, of course, is interest. Luckily, it’s not too hard to incorporate the time value of money into an analysis of mortgage points.
The mortgage point problem as a stream of cash flows
The key to analyzing the mortgage point problem properly is to realize the benefits and costs as a stream of cash flows. This is the same technique that a company should use to make a go/no-go decision about a potential project. This may seem strange because there are no cash inflows—there’s only cash leaving your pocket and going to the bank. I’ll come back to that in a second. First, let’s make sure we have a spreadsheet set up to help with the calculations.
For the rest of this post, you’ll want to have my mortgage workbook handy. You can find a solved copy of the workbook at the bottom of the page. Rather than give step-by-step instructions on how to update the workbook from the previous article, I’ll just give you the highlights. The first step is to enter the inputs for your “baseline” mortgage. Next, copy that tab to build the mortgage table with points.2 I added a few new cells to the top of the second tab to capture the details about the points. The interest rate for the mortgage with points should link to the baseline interest rate. Finally, make a third tab to record the cash flows.
Speaking of cash flows, let’s figure out how to model them in our case. As I said earlier, it appears that there’s only money going out, regardless of how many points you buy. While that’s true, a fundamental principle of investment decisions is that you want to consider cash flow on an incremental basis. This means that cash coming in or going out is always relative to what it would be if you did not undertake the project. If you’re deciding whether to buy mortgage points, the premise is that you are going to have a mortgage. Therefore, a reduction in your monthly payment should be viewed as a cash inflow. With that in mind, there are three differences in the two mortgage tables that lead to cash flows for this problem.
The upfront cost of the mortgage points is a cash outflow
The monthly payment reduction is a cash inflow
When you sell your house, the difference in the amount owed is a cash inflow (more on that later)
A quick aside on taxes… In general, mortgage interest can be deducted from your income taxes. That includes prepaid interest. A tax deduction of several thousand dollars could be significant and probably deserves to be included in the analysis. (This is especially true while the standard deduction is very high, as it could be the difference between itemizing and not.) That said, it’s too complicated to model here. Also, please refer to the second sentence of the post.
Now let’s get back to filling in our cash flow table. As you can see in the picture below, I started by making one column for month and one column for each of our cashflow sources, as well as a total cash flow column. Since point cost is a cash outflow, we put the negative of the upfront point payment in Month 0 (row 4). All subsequent rows are 0. PMT Delta is equal to 0 in Month 0 because no payments have been made at that point. For each subsequent month, it should be payment (no points) minus payment (with points), which is positive.
Why do we care about EB (ending balance)? Well, if you decide to sell your house before you’ve paid off the mortgage, the ending balance after your most recent payment is the amount that you still owe the bank. They’ll be first in line (maybe second behind the IRS) to take that amount out of the proceeds from the sale of the house. Therefore, any differences in EB with a points purchase lead to cash flow differences when you sell the house. At any given time, if the ending balance with points is smaller, then you would pay the bank less, so the difference from baseline would be an inflow. Therefore, we should type ending balance (no points) minus ending balance (with points), just like for payment.
Filling out the Total Cash Flow column is a little tricky. We definitely want to add Point Cost and PMT Delta in each month. As for ending balance, this only applies if you sell the house (or if you pay it off early). This means that we need to have a new input, Sale Period, representing the number of months you intend to keep the mortgage. For example, if you plan to die in your house, just put 360 (or whatever the term of your mortgage is). If you plan to sell the house or pay off the mortgage in 10 years, put 120. Using a nested if statement, you can then fill in the Total Cash Flow column according to whether the current month is less than, equal to, or greater than the Sale Period. In the third case, the cash flow is 0, since you no longer have the mortgage.
Computing IRR
Once you set up your stream of cash flows, the next step is to discount them to the present day. If you’re like me, you probably don’t have an accurate idea of your cost of capital. Instead, what you can do is find the discount rate at which you break even on the stream of cash flows. This is called the internal rate of return (IRR). More precisely, an IRR is a discount rate for which the net present value (NPV) of the stream of cash flows equals 0.
Notice that I wrote “an” IRR instead of “the” IRR. I did so because IRR is not unique, in general. The reason—as I discussed in this previous post—is that IRR is the solution to a polynomial equation. You can have more than one solution, if the stream of cash flows has more than one change in sign. Luckily, in this case, that won’t happen. To prove this, you can show that the ending balance after each month is less for a loan with a smaller interest rate, assuming that the loan amount and term are the same. (That was unpleasant, so take my word for it.) This means that the cash flows in all months after month 0 will be positive, regardless of the Sale Period. With that technicality out of the way, all we have to do is use Excel’s IRR function to compute the IRR. Because we were careful to put 0s for all cash flows after the Sale Period, we can use a static formula IRR(E4:E364) that captures the cash flows from months 0 to 360, regardless of when you sell the house. (A cashflow of 0 at the end of the stream of payments has no impact on IRR.)
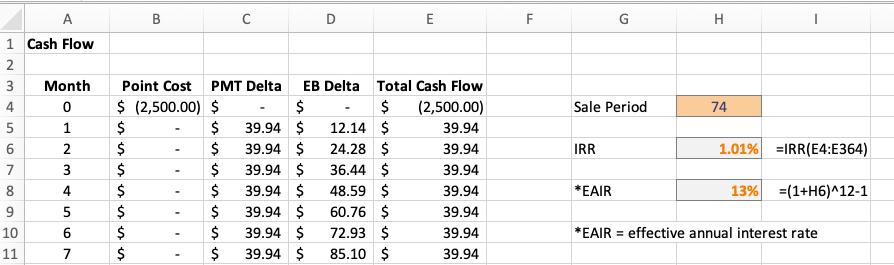
Using the parameters from the above example yields an IRR of about 1.01%. If you’re thinking that sounds low, remember that Excel’s formula calculates IRR based on the payment interval over which your cash flows occur. In this case, that would be months. To come up with an annual figure, you can use the following formula:
where EAIR stands for effective annual interest rate. Alternatively, you could sum up the cash flows for each year and then use Excel to compute the IRR for the annual cash flows. That number will be a little bit smaller because you miss the interest compounding throughout each year.
In our example, if you purchased points for $2,500 and sold the house after 74 months, the annualized rate of return would be about 13%. The question is then how that annual performance compares to other opportunities for investing $2,500 today. Again, I can’t stress enough that this is not financial advice. In addition to tax deductions mentioned above, there are other variables that may affect your situation that I have not accounted for.
When do mortgage points give you the most bang for your buck?
Using the attached workbook, you can now analyze any offer of mortgage points that you receive. To close the post, I want to investigate when mortgage points are more or less valuable. To do that, I’m going to parametrize some of the key variables that impact the sequence of cash flows: baseline interest rate, sale period, and BP reduction. (R code, generated with love by my research associate Chat-GPT, available on request.)
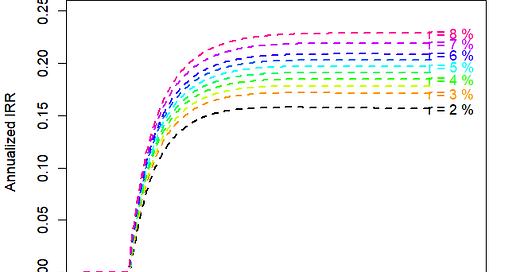
Per the picture below, the first key takeaway is that interest rate deductions are more valuable the higher the baseline rate. This surprised me a little because a 25 BP reduction seems more significant for a 2% loan than for an 8% loan. However, the monthly payment on a 2% loan is already small enough that the incremental benefit of reducing the rate is much smaller.
A second takeaway is that IRR increases very steeply each month you keep the house past the payback period, but only for 3-4 years past that point. In other words, if you are confident that you’ll keep the house for at least as long as the payback period (which you can compute before deciding on the points) plus 3-4 years, then you can be pretty sure that you’ll capture the value of purchasing points, at least for a 25-BP point. This makes sense because of how discounting works: the further out in the future a payment is, the less valuable it is to you now. This is compounded by the fact that the EB delta starts to shrink towards the end of the loan (since the ending balance after month 360 is 0, regardless of interest rate).
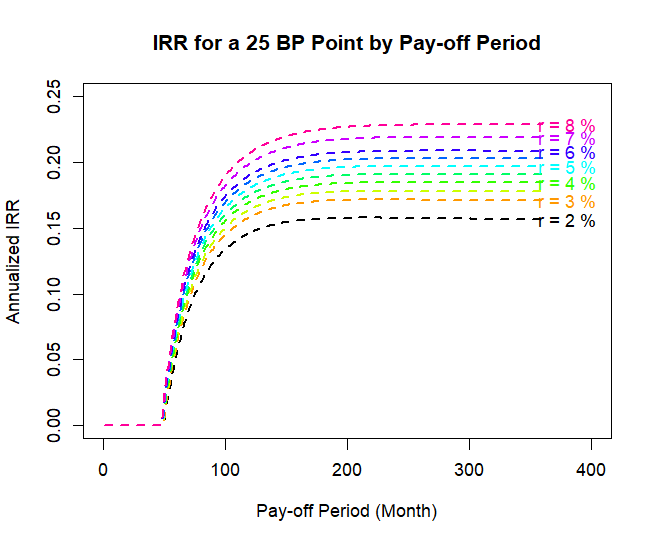
The next thing I looked at was the impact of changing the reduction in rate that one point gets you. This variable captures the “price” of the points for the purchaser. Why? The cost of one point is typically 1% of the loan amount. If we take that as fixed, then the bank can make points more or less valuable only by changing the amount that they reduce the interest rate for that 1%. Investopedia says that the typical range is one eighth to one quarter of a percent, i.e. 12.5 - 25 basis points. Unsurprisingly, this dramatically impacts the IRR of the points investment. Per the graph below, a 12.5-BP point has an IRR of about 8% for an 5% mortgage, compared to about 19% for a 25-BP point. My takeaway is that mortgage points are much better deals for 25 basis point reductions than for 10-15 basis point reductions. While that sounds obvious, it’s nice to have a benchmark in mind when reviewing an offer.

A lower IRR is not the only consequence of reducing the BP reduction value. As the picture demonstrates, the IRR curve also flattens out. This means that if you want to realize the value of purchasing points, you have to wait longer to pay off the mortgage or sell the house at lower BP reduction levels. Of course, the payoff period itself is pushed to the right if you reduce your interest rate discount (as it reduces the monthly payment delta). But even beyond that month, it appears that you would want to hold the mortgage for 6-8 additional years to get close to the peak IRR value.
In conclusion, mortgage points merit consideration when you’re applying for a home loan. If you can float the up-front cost, the reduction in monthly payment is significant, especially if one point earns you a 25-basis point reduction in interest rate. More generally, I hope you see the value of modeling investment decisions as a sequence of cash flows. Remember to think carefully about what cash flows look like with and without the investment! If you enjoyed today’s post, please subscribe and share with your network. Feel free to leave comments or questions below.
One “basis point” is equivalent to 0.01%. Although this seems like tedious jargon, it actually reduces ambiguity. If you get a 1% reduction on a 4% loan, does that mean 3% or 3.96% (1% of 4%)? If you instead say 100 basis points, then it’s clear that you mean your new rate is 3%.
When you copy the tab, the cell names that I used in the original tab will also be copied. This leads to the same label being used for two different cells, with the original tab superseding the second (very unfortunate). I recommend deleting the names in the second tab, which will require recreating the formulas based on standard cell references (e.g., E5). To delete the names, go to Formulas > Name Manager. Then, delete all the names that have =’Mortgage Table with Points’… in the “Refers To” column. I apologize for the inconvenience and promise to do better next time.