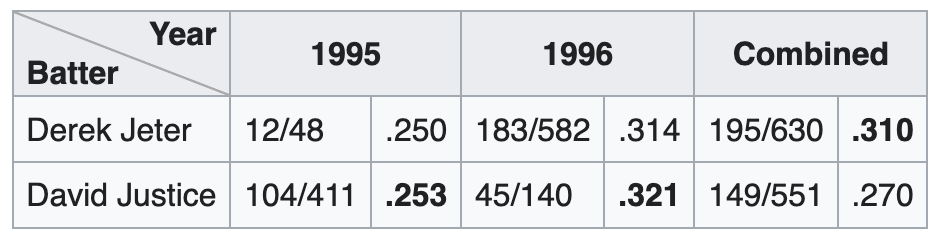D'oh!
A quick look at Simpson's paradox, a statistical trap for the lazy (and overzealous)
Let’s say you run a company and employ two salespeople, Aaron and Bill. You learn that Aaron converted 36% of his leads last quarter, whereas Bill only converted 32%. Not willing to tolerate losers in your company, you decide to drop the axe on Bill.
Now suppose that you have two types of customers: enterprise and end user. Bill closed 25% of end users, compared to 20% for Aaron. Bill also closed 43% of enterprise customers, compared to only 40% for Aaron. In this scenario, clearly it’s Aaron who needs to go.
What if I told you that these scenarios were one and the same? Surely that’s not possible, right? There’s no way that Bill can outperform Aaron on both customer types and still end up with a lower overall conversion rate. Take a look at the following table to see that it is indeed possible.
This is an example of what’s known as Simpson’s paradox. Most generally, the paradox refers to a trend in a dataset that disappears or reverses when data is disaggregated. The most common (and dangerous) way for the paradox to manifest is when we try to ascribe causality to frequency data. In this case, I saw that Aaron had superior conversion rates to Bill and attributed the difference to Aaron being a better salesperson. However, considering the two customer types separately tells a different story.
The totals in each cell of the table give a good indication as to what must be true to have a Simpson situation. Although Aaron and Bill each had 500 leads total, they have vastly different quantities of leads within each customer category. Bill has three times the end user leads of Aaron, but half as many enterprise leads. Enterprise leads are about twice as easy to close, so the fact that Aaron sees many more of them inflates his closure rate. So, which salesperson would you keep? It seems that Bill is better at selling to both types of customers, so he would be my choice.
Batting averages
Here’s another example, taken right from the Wikipedia entry on Simpson’s paradox. In 1995, outfielder David Justice had a higher batting average than shortstop Derek Jeter.1 The same was true in 1996. Yet, Jeter had a (much) higher average than Justice over those two years.
This is Simpson’s paradox in action again. So, what conclusion should we draw? In this case, I would say that Jeter was the more effective hitter over the span. Notice that this is the opposite conclusion from the first case. Here, I’m favoring the aggregated data over the disaggregated data. My reason for doing so—other than Jeter being a Yankees legend—is that the split into different years seems somewhat arbitrary. Let’s instead look at how Jeter and Justice fared against left-handed pitchers (LHP) and right-handed pitchers.
It is known that hitters, on average, perform better against pitchers who throw with the opposite arm. (Jeter bats righty, for example, so his average should be higher against LHP.) Therefore, the fact that Jeter has a higher average against both righties and lefties may indicate that he’s a more effective hitter (for average, at least).
I’ll close with one final stir of the pot. I confidently stated that Bill is the superior salesperson to Aaron because he had a better closure rate on both end users and enterprise customers. But why stop there with disaggregation? Maybe if you consider new and existing customers within each category, the trend will reverse and Aaron will seem like the better salesperson. The moral of the story is that you should be very careful when claiming a causal relationship between two variables. You never know what other explanations are lurking in the data.
Fun fact: I was in attendance for both Justice’s (November 2001, old stadium) and Jeter’s (September 2014, new stadium) last games at Yankee Stadium as a Yankee. It was Jeter’s last game at Yankee stadium, period, but Justice played two more there in 2002 as a member of the Oakland A’s. If you’ve seen Moneyball, Justice is the guy with the bad knees.